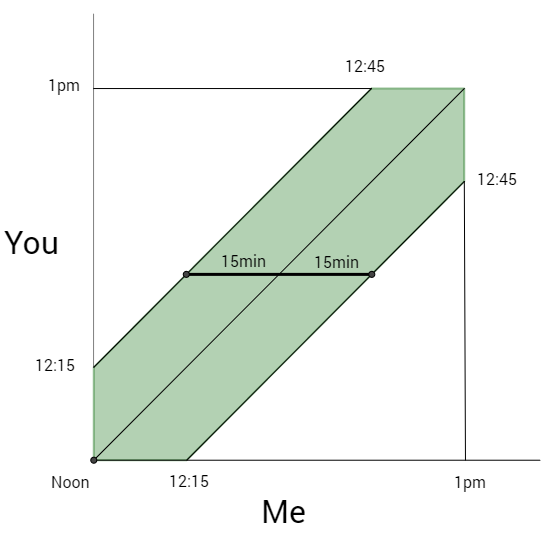
On a lovely spring day, you and I agree to meet for a lunch picnic at the fountain in the center of our favorite park. We agree that we’ll each arrive sometime from noon and 1 p.m., and that whoever arrives first will wait up to 15 minutes for the other. If the other person doesn’t show by then, the first person will abandon the plans and spend the day with a more punctual friend. If we both arrive at the fountain at an independently random time between noon and 1, what are the chances our picnic actually happens?
Solution:
We visualize the possible pairs of arrival times as a square. The green region is where we arrive within fifteen minutes of one another, and so are able to meet. Since the area of the whole graph is one, the probability that we meet is the area of the green region, which is easiest to calculate by subtracting from one the area of the white triangles. Pushed together, they form a square of side 3/4 and area 9/16, and so the probability that we meet is 7/16.
Extra Credit
Suppose there are $N$ people and that they stay a proportion $R$ of the hour. What is the chance that all of them will be there at the same time?
(Suggested by @NM_Solver on twitter)
Call one of the people A. We are going to calculate the probability that A arrives first and everyone meets. We will then multiply that probability by $N$ to get our answer.
Call the time A arrives, $t$. For all to meet, all of the $N-1$ others must arrive between $t$ and $t+R$. If $t \leq 1-R$, then each has $R$ chance of doing so, and if $t \geq 1-R$, then each has $1-t$ chance.
There is, then, a $(1-R)R^{N-1}$ chance of A arriving before $1-R$ and everyone arriving within $R$ afterwards.
To calculate the chance of everyone meeting when A arrives first and arrives after $1-R$, we need to integrate over the possible values of $t$:
\[\int_{t=1-R}^1 (1-t)^{N-1} dt = \bigg[_{t=1-R}^{1} - \frac{(1-t)^N}{N} \bigg] = \frac{R^N}{N}\]Putting it all together, the probability that they all meet is:
\[P = N \times \bigg[ (1-R)R^{N-1} + \frac{R^N}{N} \bigg] = NR^{N-1} - (N-1)R^N\]Here are some values of $P$, for values of $R$ heading columns and $N$ heading rows.
| 0.1 | 0.25 | 0.35 | 0.45 | 0.5 | |
|---|---|---|---|---|---|
| 2 | 0.19 | 0.4375 | 0.5775 | 0.6975 | 0.75 |
| 3 | 0.028 | 0.15625 | 0.28175 | 0.42525 | 0.5 |
| 4 | 0.0037 | 0.05078125 | 0.12648125 | 0.24148125 | 0.3125 |
| 5 | 0.00046 | 0.015625 | 0.0540225 | 0.13122 | 0.1875 |
| 6 | 0.000055 | 0.004638671875 | 0.02232179688 | 0.06919804688 | 0.109375 |
| 7 | 0.0000064 | 0.001342773438 | 0.009007501563 | 0.03570619219 | 0.0625 |
| 8 | 0.00000073 | 0.0003814697266 | 0.003570830977 | 0.01812296848 | 0.03515625 |
| 9 | 0.000000082 | 0.0001068115234 | 0.001396162742 | 0.009080167711 | 0.01953125 |
| 10 | 0.0000000091 | 0.00002956390381 | 0.0005398871249 | 0.004502249823 | 0.0107421875 |
Verified by numerical simulation:
from random import random
N = 5
R = .25
reps = 1000000
accum = 0
for rep in range(reps):
Arrivals = []
for i in range(N):
Arrivals.append(random())
Picnic = 1
for i in range(N):
for j in range(N):
if abs(Arrivals[i]-Arrivals[j]) > R:
Picnic = 0
if Picnic == 1:
accum += 1
print(accum/reps)