You play a game with four balls: One ball is red, one is blue, one is green and one is yellow. They are placed in a box. You draw a ball out of the box at random and note its color. Without replacing the first ball, you draw a second ball and then paint it to match the color of the first. Replace both balls, and repeat the process. The game ends when all four balls have become the same color. What is the expected number of turns to finish the game?
Solution
A possible “situation” is a numerical description of the division of the balls in to same-color groups. With $4$ balls we can label the possible situations $[1,1,1,1]$ (the situation at the start), $[2,1,1]$, $[2,2]$, $[3,1]$, and $[4]$ (the situation at the end).
Each situation has a readily-determined probability of being followed by each other situation. For example, from $[2,1,1]$ to remain in the same situation you can get both of the same-colored balls ($1/2 \times 1/3$, or $1/6$ chance of that), or you can get one of the loners and then one of the two same-colored balls ($1/2 \times 2/3$, or $1/3$ chance of that), for a total probability of $1/2$. Here are all the cases:
$[1,1,1,1]$: Probability $1$ of $[2,1,1]$.
$[2,1,1]$: Probability $1/6$ of $[2,2]$, $1/2$ of $[2,1,1]$, and $1/3$ of $[3,1]$.
$[2,2]$: Probability $1/3$ of $[2,2]$, and $2/3$ of $[3,1]$.
$[3,1]$: Probability $1/2$ of $[3,1]$, $1/4$ of $[2,2]$, and $1/4$ of $[4]$.
Where $A$, $B$, $C$, and $D$ are the expected number of turns to yield $4$ starting with each of these situations, in the order just listed, then, we have the following system of equations:
$A = 1 + B$
$B = 1 + B/2 + C/6 + D/3$
$C = 1 + C/3 + 2D/3$
$D = 1 + C/4 + D/2$
Tedious minutes later, or in an instant after entering the equations into an online system of equations solver, we find that $A$, $B$, $C$, and $D$ are $9$, $8$, $7$, and $11/2$. So we expect the game to take $9$ turns.
Which, interestingly enough, is $(4-1)^2$. Hmmm . . .
Extra Credit
What if there are more balls and more colors?
Let’s ask the question, given a particular color, on average how many turns does it take for that color to win, given that it does win? This will answer the puzzle question, because all colors are alike in this respect.
Let $E_i$ be the average number of turns from now for the color to win when currently there are $i$ balls of that color. Then, where $B$ is the number of Balls:
\[E_B = 0\]To get an expression for $E_1$, we add $1$ (for the first turn) to the weighted average of the expectations of the possible outcomes of the first turn that are consistent with the color winning (namely, staying at $1$ and going to $2$). The weights are the conditional probabilities that the outcomes occur given that we are ultimately going to win. The probability of $A$ conditional on $B$ is:
\[P(A | B) = \frac{P(A \& B)}{P(B)}\]In this case, the probability that we stay put at $1$ conditional on our winning is the unconditional probability that we stay put now times the probability that in that case we win, divided by the unconditional probability that from this situation we win:
\[\left(\frac{B-1}{B} \cdot \frac{B-2}{B-1} \cdot \frac{1}{B}\right) \div \frac{1}{B} = \frac{B-2}{B}\]And the probability that we move to $2$ conditional on our winning is:
\[1 - \frac{B-2}{B} = \frac{2}{B}\]So,
\[E_1 = 1 + \frac{B-2}{B}E_1 + \frac{2}{B}E_2\]Solving,
\[E_1 = E_2 + \frac{B}{2}\]For every intermediate $i$, the expectation $E_i$ is $1$ plus a function of the two neighboring expectations $E_{i-1}$ and $E_{i+1}$ and of $E_i$ itself, weighted by how likely it is to color one more ball, or one fewer, or remain at $i$ on the next turn, again conditional on our winning.
The probability that we’ll now move to $i-1$, given that we’ll go on to win is:
\[\left(\frac{B-i}{B}\cdot\frac{i}{B-1} \cdot \frac{i-1}{B}\right) \div \frac{i}{B} = \frac{(B-i)(i-1)}{B(B-1)}\]The probability of now moving to $i+1$, given an eventual win, is:
\[\left(\frac{i}{B} \cdot \frac{B}{B-1} \cdot \frac{i+1}{B}\right) \div \frac{i}{B} = \frac{(B-i)(i+1)}{B(B-1)}\]And the probability of staying put given a win is:
\[1 - \frac{(B-i)(i-1)}{B(B-1)} - \frac{(B-i)(i+1)}{B(B-1)} = 1- \frac{2i(B-i)}{B(B-1)}\]Therefore,
\[E_i = 1 + \frac{(B-i)(i-1)}{B(B-1)}E_{i-1} + \left(1- \frac{2i(B-i)}{B(B-1)}\right)E_i + \frac{(B-i)(i+1)}{B(B-1)}E_{i+1}\] \[E_i = \frac{i-1}{2i}E_{i-1} + \frac{i+1}{2i}E_{i+1} + \frac{B(B-1)}{2i(B-i)}\]Rearranging,
\[2iE_i = (i-1)E_{i-1} + (i+1)E_{i+1} + \frac{B(B-1)}{B-i}\] \[(i+1)E_{i+1} - iE_i = iE_i - (i-1)E_{i-1} - \frac{B(B-1)}{B-i}\]Let $\Delta_i = (i+1)E_{i+1} - iE_i$. Remembering that $E_1 = E_2 + \frac{B}{2}$, we know that,
\[\Delta_1 = 2E_2 - 1E_1 = E_1-B\] \[\Delta_i = E_1-B - \sum_{j=2}^{i}\frac{B(B-1)}{B-j}\]And remembering that $E_B = 0$,
\[BE_B = 1E_1 + \sum_{i=1}^{B-1} \Delta_i\] \[= E_1 + \sum_{i=1}^{B-1} \left( E_1-B - \sum_{j=2}^{i}\frac{B(B-1)}{B-j}\right) = 0\] \[E_1 + (B-1)(E_1-B) - B(B-1) \sum_{i=2}^{B-1} \sum_{j=2}^{i}\frac{1}{B-j} = 0\] \[E_1 = (B-1)\left(1 + \sum_{i=2}^{B-1} \sum_{j=2}^{i}\frac{1}{B-j}\right)\]That double-sum can be simplified to a single sum, by putting in the numerator of the summed fraction an expression for how many times the original fraction would occur in the expansion of the double-sum:
\[\sum_{i=2}^{B-1} \sum_{j=2}^{i}\frac{1}{B-j} = \sum_{i=2}^{B-1}\frac{B-i}{B-i} = \sum_{i=2}^{B-i}1 = B-2\]Thus,
\[E_1 = (B-1)^2\] \[E_2 = (B-1)^2 - \frac{B}{2}\]And for arbitrary $i$,
\[iE_i = 2E_2 + \sum_{j=2}^{i-1} \Delta_j\] \[= 2\left((B-1)^2-\frac{B}{2}\right) + \sum_{j=2}^{i-1} \left( (B-1)^2-B - \sum_{k=2}^{j}\frac{B(B-1)}{B-k}\right)\]Calling the second addend $X$,
\[X = (i-2)((B-1)^2-B)-B(B-1)\sum_{j=2}^{i-1}\sum_{k=2}^{j} \frac{1}{B-k}\] \[= (i-2)((B-1)^2-B)-B(B-1)\sum_{j=2}^{i-1} \frac{i-j}{B-j}\] \[E_i = (B-1)^2 - B + \frac{B}{i}\left(1 - (B-1) \sum_{j=2}^{i-1}\frac{i-j}{B-j} \right)\] \[= (B-1)^2 - \frac{B-1}{i}\sum_{j=1}^{i-1}\frac{i-j}{B-j}\]If there are $B$ colors as well as balls, the expected length of the game is $E_1$. If there are $C$ colors evenly distributed among the balls, the expectation is $E_{B/C}$.
For a game with 100 balls, the graph below shows how the expected number of turns until a color wins, assuming it will, depends on how many balls are currently of that color. (Perhaps surprisingly, $E_{99}$ is approximately $419$.)
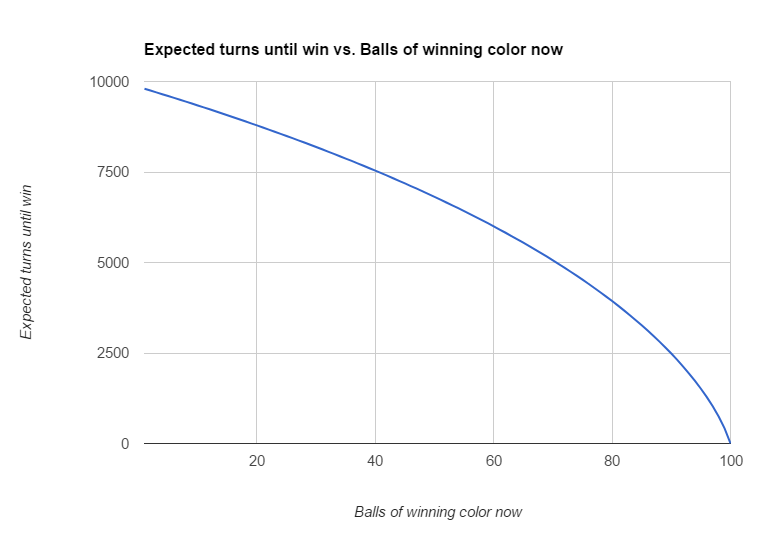
By the way, it’s possible to replace the sum in the above explicit expression for $E_i$ with what look like more closed-form expressions employing the digamma function or the harmonic numbers, but any apparent advantage of the simple notation is illusory, given how those functions are defined.
See this similar and more concise solution by Sawyer Tabony.