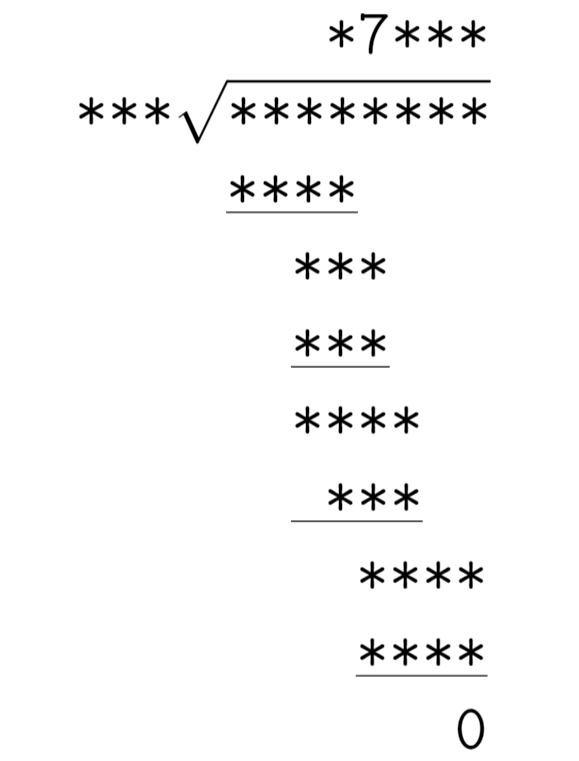
In the long division below, each asterisk represents a whole number — any digit from 0 to 9. Reconstruct all the calculations, given that there is no remainder.
Solution
Start by labeling the numbers:
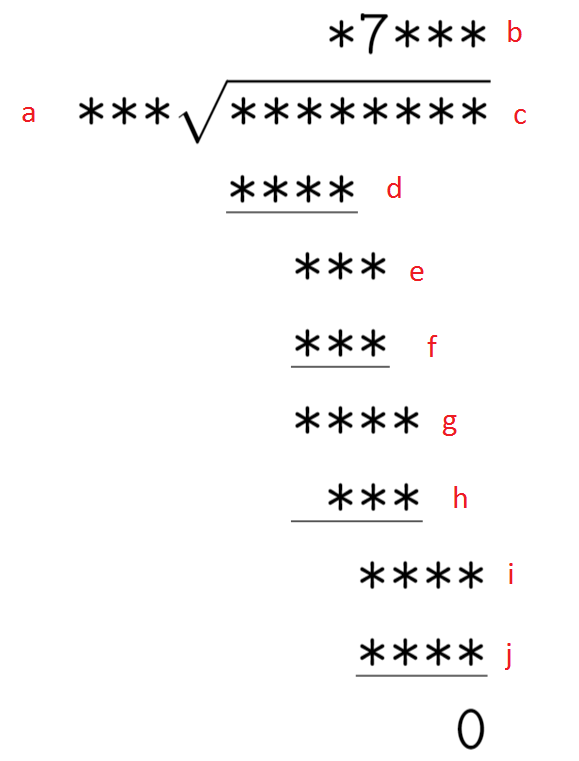
Since $f$, which is less than $1000$, is $7$ times $a$, $a$ is $142$ or less.
Observing that $i$ required bringing down two digits, we know that the number formed by the first three digits of $i$ is less than $a$ (and so the penultimate digit of b is $0$). Thus $g$ (which is at least $1000$) minus $h$ must be $14$ or less, and so:
\[986 \leq h \leq 999\]Now, $h$, having three digits, is $a$ times either $7$ or $8$. If $7$, then it is equal to $f$. But $f$ subtracted from $e$, another three-digit number, yields a three digit number, which is impossible if $f$ is $900$ or above. So $h$ is $a$ times $8$, and, being divisible by 8, can only be $992$, which makes $a$ $124$.
Therefore, the four-digit $d$ and $i$ are each $9$ times $a$, and so $b$ is $97809$, and so $c$ (which is $a$ times $b$) is $12128316$, and the rest of the numbers fall into place easily.