Fans of Dungeons & Dragons will have fond feelings for four-sided dice, which are shaped like regular tetrahedrons. Some might have noticed, in those long hours of fantasy battle, that if you touch five of these pyramids face-to-face-to-face, they come agonizingly close to forming a closed pentagon. Alas, there remains a tiny angle of empty space left between two of the pyramids. What is the measure of that angle?

Five tetrahedrons.

(fivethirtyeight.com)

Solution

First we determine the dihedral angle (labeled $\theta$ in the diagrams) between faces of a regular tetrahedron:

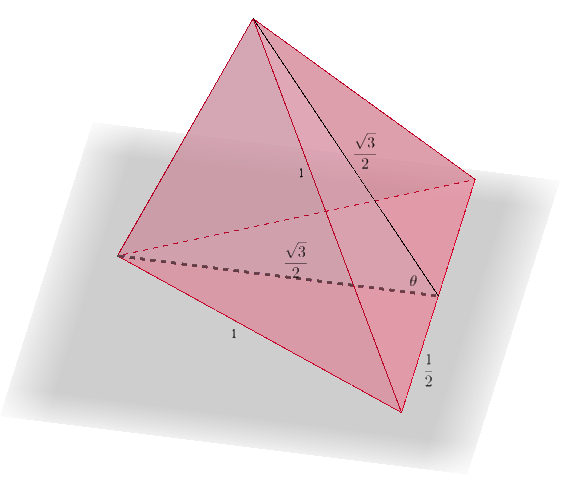
One Tetrahedron.

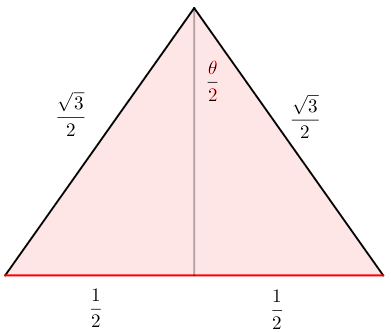
Tetrahedron section.

\[\frac{\theta}{2} = \arcsin{\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}}\] \[\theta = 2\arcsin{\frac{\sqrt{3}}{3}} \approx 70.53^\circ\]

The five tetrahedra together take up five times that angle, and so what’s left over is:

\[360 - 5 \times \theta \approx 7.356^\circ\]

To form a complete pentagonal loop, the dihedral angle would have to be $72^\circ$, which we could achieve by lengthening the circumferential sides of the tetrahedra from $1$ to $\sqrt{3}\sin{36}$, or about $1.018$. Voila: no more agony!

Completed pentagonal ring.