Running Buddies

Let’s say there are $N$ people going for a run, and assume that each person’s preferred running speed, call it $X_i$, is independent and normally distributed, with a mean of $\mu$ and a variance of $\sigma^2$. Or, mathematically,

\[X_i \sim N(\mu,\sigma^2)\]

Now, for any given person, let’s assume that the person has a running buddy if there’s another person in the group whose preferred speed is about the same as theirs. Specifically, we’ll say that person $i$ and person $j$ can be running buddies if their preferred speeds are within some number $s$ of each other — that is, if $|X_i - X_j| \leq s$.

How large does $N$ need to be before the probability of each person having a running buddy is $99$ percent? (Assume $\mu$, $\sigma^2$ and $s$ are fixed.)

(fivethirtyeight)

Solution

There are at least two ambiguities here.

The first is that runners actually get to run with buddies only if they are partitioned into buddy groups, such that for each group, any two members of the group are within $s$ in speed (and they run together, say, at the average of their speeds). But that not only makes the problem very complicated, it also makes it not always true that a runner has a buddy if there’s another runner within $s$ in speed. So we’ll assume that runners “having buddies” doesn’t entail that they can all run with a buddy, but merely that there are other runners within $s$ in speed.

The second ambiguity is in the quantifier “each.” Are we looking for $99\%$ probability that all runners have buddies, or are we looking for a $99\%$ probability that a randomly selected runner has a buddy? Either interpretation is possible semantically, but the choice of the phrase “each person” over “every person” and “all people” suggests that we are focusing on per-person probabilities, i.e., the latter interpretation, which is what we therefore will assume.

Choose units so that $\mu$ is $0$ and $\sigma$ is $1$ (true, this gives half of the runners negative speeds, but positive probability of negative values is inevitable with any normal distribution). Think of it as the speed relative to the average runner.

Let my speed be $X$. Then, the chance $B_X$ that a given other runner is my buddy is the probability that their speed is between $X - s$ and $X + s$, which, where $\Phi$ is the cumulative distribution function for the standard normal distribution (which is the distribution of each $X_i$), is:

The chance $O_x$ that, with speed $X$, I have at least one buddy is one minus the chance that all $N - 1$ other runners are not buddies:

The chance that my speed is between $X$ and $X + dX$ is

where $f$ is the probability density function for the standard normal distribution:

So the chance that I have a buddy is:

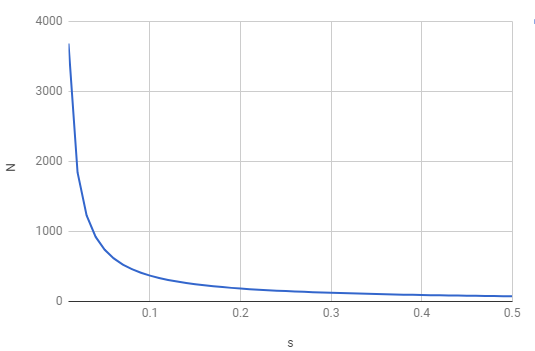
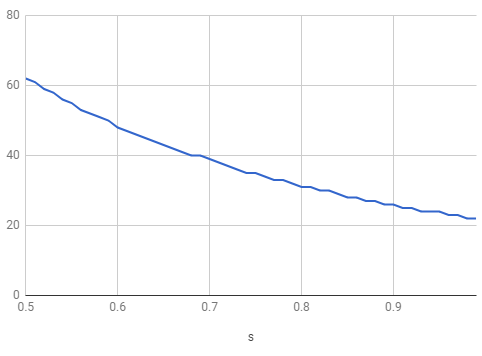
There’s no hope of a closed-form solution to the integral, so we evaluate it numerically, for various $s$ and $N$ so as to identify, for each value of $s$ we examine, the least $N$ for which the integral matches or exceeds $.99$. The results are charted below. They can be read in a general way, as identifying how many runners are needed for a randomly selected runner to have a $.99$ chance of there being another runner within $s$ standard deviations of their speed.

Code (Python):

from math import exp,pi,sqrt,erf

def integrate(lowLimit,highLimit,function,step):
	accum = 0
	x = lowLimit
	while x <= highLimit:
		accum += step * function(x)
		x += step
	return accum

def phi(x):
    #'Cumulative distribution function for the standard normal distribution'
    return (1.0 + erf(x / sqrt(2.0))) / 2.0

def normalPDF(x,mu,sigma):
	return (1 / sqrt(2*pi*sigma**2)) * exp(-(x-mu)**2 / (2.0*sigma**2))

def buddyPDF(x):
	global s, N
	return (1 - (1 - (phi(x + s) - phi(x - s))) ** (N-1)) * normalPDF(x,0,1)

def buddyProb():
	return integrate(LOW_INT_LIMIT,HIGH_INT_LIMIT,buddyPDF,INT_STEP)

CONFIDENCE = .99
LOW_S = .01
STEP_FOR_S = -.01
HIGH_S = 1.0
LOW_INT_LIMIT = -10
HIGH_INT_LIMIT = 10
INT_STEP = .001

Ns = {}
s = HIGH_S
lastN = 1
while s >= LOW_S:
	N = lastN
	while True:
		prob = buddyProb()
		if prob >= CONFIDENCE:
			Ns[s] = N
			lastN = N
			break
		else:
			N += 1
	s += STEP_FOR_S