Spherical Triangle

I want to carve the perfect eye for my pumpkin this Halloween, but I can’t seem to make it the right size. Since symmetry is the key to beauty, the triangular eye should be equilateral and equiangular, which is easier said than done on the surface of a spherical pumpkin!

To be a proper triangle, the three corners should be connected by arcs that are “straight,” meaning they go directly from one corner to the next via the shortest possible path. (Think about air travel: When you flying from the West Coast of the U.S. to Europe, you’ll fly north of the Arctic Circle along the way, since that’s the shortest path over the Earth’s curved surface.)

I want an eye that’s one-sixteenth of the pumpkin’s surface. For such an ideal pumpkin eye, at what angle should each of the sides meet?

(fivethirtyeight)

Solution

For simplicity, we’ll work with a unit sphere (of surface area $4\pi$) and find the angle $\alpha$ needed for a spherical triangle of area $\pi/4$.

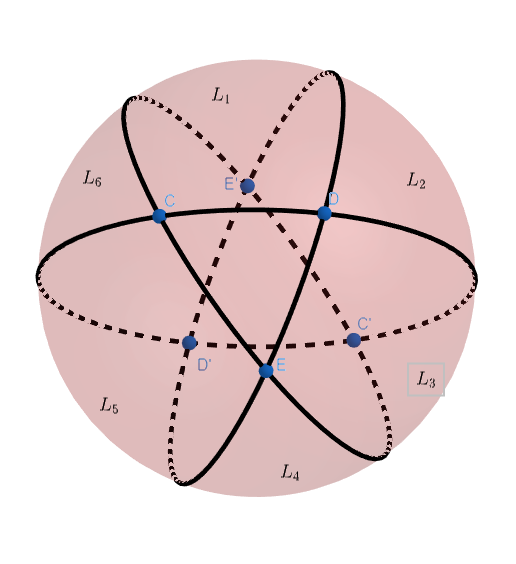
In the figure, note that the sides of the triangle lie on three great circles, each pair of which (like all pairs of great circles) intersect twice, at polar opposite points on the sphere.

A lune is a section of a sphere’s surface bounded by two such great circles. Since these circles intersect at an angle $\alpha$, the area of the lunes is $\alpha/2\pi$ times the surface area ($4\pi$) of the sphere, or $2\alpha$. Each pair (of three pairs total) of the circles determines two lunes of angle $\alpha$, for six in total.

Notice that the three circles also bound a second, congruent triangle on the far side of the sphere.

If we add the areas of all six lunes, yielding $12\alpha$, we cover the entire sphere, but in doing so we count the area $A$ of our triangle three times, and similarly for that of the second triangle, for a total over-count of $4A$. So:

If $A$ is $\pi/4$, then $\alpha$ is $5\pi/12$, or $75$ degrees.