After a long night of frivolous quackery, two delirious ducks are having a difficult time finding each other in their pond. The pond happens to contain a 3×3 grid of rocks.
Every minute, each duck randomly swims, independently of the other duck, from one rock to a neighboring rock in the 3×3 grid — up, down, left or right, but not diagonally. So if a duck is at the middle rock, it will next swim to one of the four side rocks with probability 1/4. From a side rock, it will swim to one of the two adjacent corner rocks or back to the middle rock, each with probability 1/3. And from a corner rock, it will swim to one of the two adjacent side rocks with probability 1/2.
If the ducks both start at the middle rock, then on average, how long will it take until they’re at the same rock again? (Of course, there’s a 1/4 chance that they’ll swim in the same direction after the first minute, in which case it would only take one minute for them to be at the same rock again. But it could take much longer, if they happen to keep missing each other.)
Extra credit: What if there are three or more ducks? If they all start in the middle rock, on average, how long will it take until they are all at the same rock again?
Solution
If we start at minute $0$ on the center rock, then notice that each duck is always on side rocks at odd-numbered minutes and on non-side rocks at even-numbered minutes.
There are six state-types to keep track of. We’ll want to calculate the expected remaining minutes $E_i$ given that we’re currently in a given state type $S_i$.
- Both on center rock.
- One on center, one on corner.
- On opposite corners.
- On adjacent corners.
- On opposite sides.
- On adjacent sides.
The omitted state-types of being both on the same corner or side rock are irrelevant because it’s already game-over if the ducks are in those states. $S_1$ is far from irrelevant, though, because it is the expectation we are looking for in this problem.
We can express $E_i$, for each $i$, in terms of the values $E_j$ for each $j$ such that $S_j$ is a possible successor state to $S_i$. For example, from $S_1$, we can count on at least one more minute. But there might be more than that, in particular if we next are in $S_5$ or $S_6$. Where $T_{i,j}$ is the transition probability from state $S_i$ to state $S_j$, we have:
\[E_1 = 1 + T_{1,8}E_8 + T_{1,9}E_9\]The transition probabilities can be calculated from the probabilities given in the problem. For example, $T_{1,5}$ is the number of different ways for that transition to happen ($4$, corresponding to the $4$ choices of side rock for a given duck) times the probability that things will go any given such way ($1/16$, which is the chance that the two ducks will make those particular $1/4$-probability choices), or $1/4$.
Doing this for all six state-types, we find that state-types $1$, $2$, and $5$ have identical expectations, so we can reduce the problem to a system of four equations:
\[A = \frac{1}{4}C + \frac{1}{2}D + 1\] \[B = \frac{1}{2}C + \frac{1}{2}D + 1\] \[C = \frac{2}{3}A + \frac{2}{9}B + 1\] \[D = \frac{2}{3}A + \frac{1}{9}B + 1\]This system can be solved straightforwardly by hand. Plugging the expressions for $A$ and $B$ into those for $C$ and $D$ yields two equations in two variables, which can be solved in the usual way. We thus find that $A$, which is our $E_1$ and hence our answer, is (exactly) $363/74$, or about $4.91$ minutes.
Extra Credit
For a larger number $N$ of ducks, I did not see a path to an exact expectation, so we will use a simplification. We still think of the individual ducks as moving randomly among the rocks, alternating between sides and non-sides, but ignoring history otherwise. Each side rock is chosen $1/4$ of the time at odd minutes, Since the center has twice the number of adjacent side rocks as each corner, it is chosen $1/3$ of the time at even minutes, compared to $1/6$ for corner rocks.
Then, on an odd minute, the chance that all the ducks are at one rock is $1/4^{N-1}$, and on an even minute, the chance is $1/3^N + 4/6^N$. The average of these two values is our estimate of the probability that they will be on a single rock at a given minute, and the estimated expectation for the first such minute is its reciprocal, or:
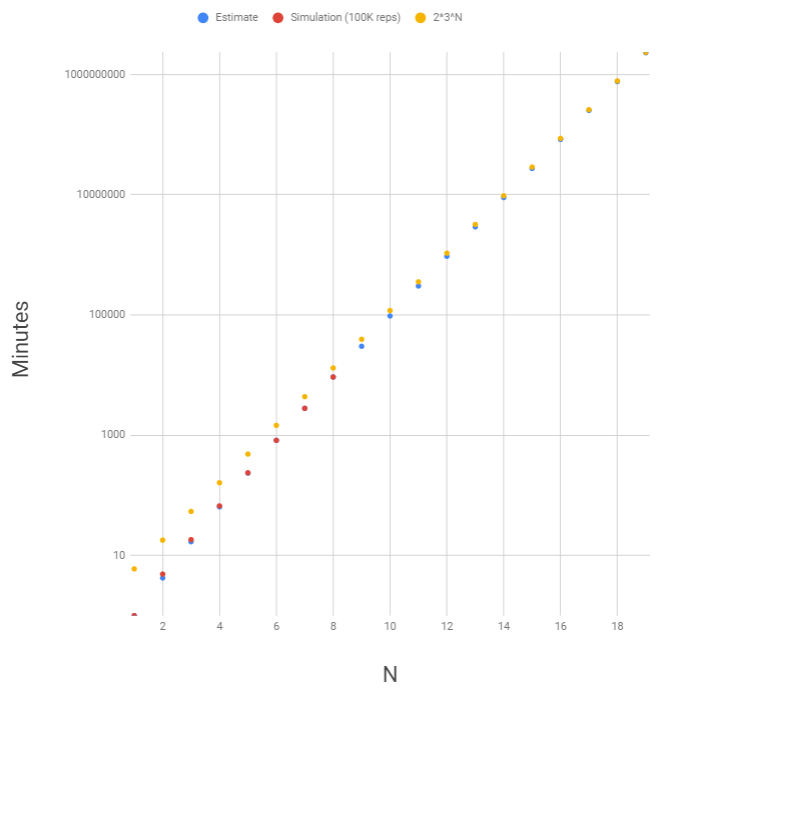
\[\frac{2}{\frac{1}{4^{N-1}} + \frac{1}{3^N} + \frac{4}{6^N}}\]For small $N$, the simplification is significant. For $N = 2$, the correct expectation value of $4.90$ is estimated at $4.24$. But it gets better proportionately, though always underestimating as far as I can tell (now “actual” values are simulations with $100,000$ repetitions):
| N | Estimate | 100K-rep Simulation |
|---|---|---|
| 3 | 16.9 | 18.4 |
| 4 | 64.4 | 66.9 |
| 5 | 237 | 234 |
| 6 | 822 | 822 |
| 7 | 2795 | 2797 |
| 8 | 9266 | 9271 |
Since each duck has a $1/3$ chance of reaching the center rock on every even-numbered second, the estimate for the first time all the ducks meet at the center rock is $2\cdot3^N$. For large $N$, meeting on other rocks becomes vanishingly improbable compared to $1/3^N$, and so $2\cdot3^N$ is the limiting expected meeting time.