Robert’s daughter has a set of Magna-Tiles, which, as their name implies, are tiles with magnets on the edges that can be used to build various polygons and polyhedra. Some of the tiles are identical isosceles triangles with one 30 degree angle and two 75 degree angles. If you were to arrange 12 of these tiles with their 30 degree angles in the center, they would lay flat and form a regular dodecagon. If you were to put fewer (between three and 11) of those tiles together in a similar way, they would form a pyramid whose base is a regular polygon. If Robert wanted to maximize the volume contained within the resulting pyramid (presumably to store as much candy for his daughter as possible), how many tiles should he use?
Solution
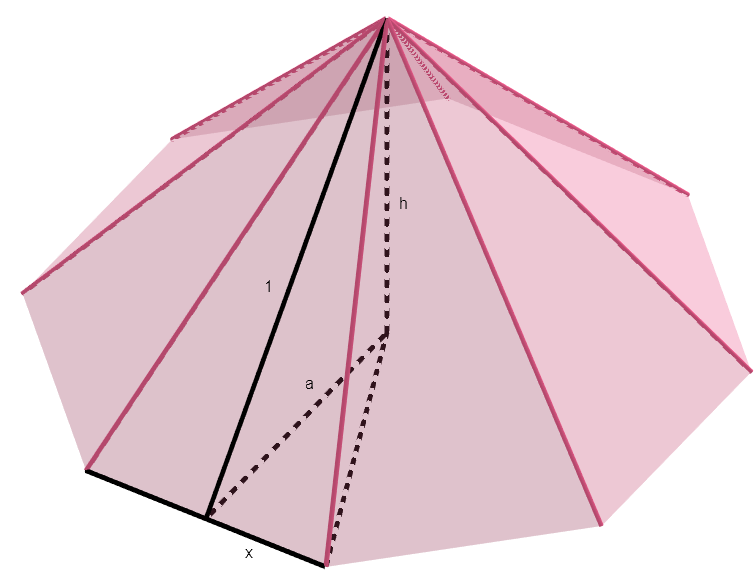
Suppose the tiles, of long dimension $1$, are such that they would form a flat $N$-gon (in the puzzle as given, $N$ is $12$). Let $x$ be half the short dimension, or $\tan{\frac{\pi}{N}}$.
If we form a pyramid with a proportion $p$ of the $N$ tiles, the base is a regular $pN$-gon with apothem $a$:
\[a = x \cot{\frac{\pi}{pN}} = \tan{\frac{\pi}{N}}\cot{\frac{\pi}{pN}}\]The height:
\[h = \sqrt{1 - a^2} = \sqrt{1 - \tan^2{\frac{\pi}{N}}\cot^2{\frac{\pi}{pN}}}\]The area of the base:
\[A = pNxa = pN\tan^2{\frac{\pi}{N}}\cot{\frac{\pi}{pN}}\]Finally, the volume:
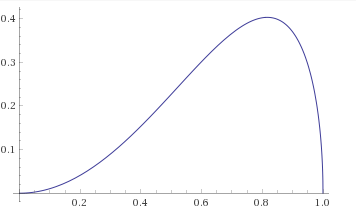
\[V = \frac{1}{3}Ah = \frac{1}{3} pN \tan^2{\frac{\pi}{N}} \cot{\frac{\pi}{pN}} \sqrt{1 - \tan^2{\frac{\pi}{N}}\cot^2{\frac{\pi}{pN}}}\]For the original puzzle, we find that $V$ is maximized when $10$ tiles are used:
As $N$ increases, the angles in the formula for $V$ decrease. For small $x$, $\tan{x}$ approaches $x$ and $\cot x$ approaches $\frac{1}{x}$, so:
\[V \rightarrow \frac{\pi}{3} p^2 \sqrt{1-p^2}\]That looks suspiciously simple, and indeed there is a more direct way of reaching it. At the limit, the problem is equivalent to this: you have a paper disc out of which you cut a pie slice and form the remainder, which is some proportion $p$ of the circle, into a cone. What value of $p$ maximizes the cone’s volume?
Choose a disc with radius $1$. Then the circumference of the cone’s base is $2\pi p$, and so its radius is $p$, and its area is $\pi p^2$. Its height is then $\sqrt{1-p^2}$ and so its volume is:
\[V = \frac{\pi}{3}p^2 \sqrt{1-p^2}\]To find the maximum of this function of $p$:
\[\frac{d}{dp^2} \left( p^2 \sqrt{1-p^2} \right) = 0\]Using the product and chain rules for differentiation,
\[\sqrt{1-p^2} - \frac{p^2}{2\sqrt{1-p^2}} = 0\] \[p = \sqrt{\frac{2}{3}}\]So $V$ attains its maximum value of $\frac{2\pi}{9\sqrt{3}}$ (about $.403$) at $p = \sqrt{\frac{2}{3}}$ (about $.812$). Note that this fraction of $12$ is about $9.74$, the closest integer to which is, as we might expect, our observed optimal tile-count of $10$.
$V$ versus $p$: