Perfect War

Assuming a deck is randomly shuffled before every game, how many games of War would you expect to play until you had a game that lasted just 26 turns?

fivethirtyeight.

Solution

There are $52!$ different, equally likely deals. If we can find the number of different, perfect deals, we can divide the former by the latter number to get our expectation (which is the inverse of the probability of getting a $26$-turn game). We’ll count the perfect deals in which player 1 wins, and then double that number.

We will use a recurrence to calculate the number of perfect (for player 1) partial deals that lead to a given game state, where a state lists the number of card values of which just one card remains, of which two remain, three, and four. So we’ll use $M(a_1,a_2,a_3,a_4)$, or $M(\mathbf{a})$, to mean the number of perfect deals that lead to $\mathbf{a}$, starting from the initial state of $(0,0,0,13)$. Our goal is to find $M(0,0,0,0)$, the number of perfect deals of the whole deck. Of course $M(0,0,0,13)$ is $1$.

We can calculate values of $M(\mathbf{a})$ from those of $M$ at all possible preceding states. $M(\mathbf{a})$ is a sum: for each $\mathbf{a^p}$ that describes a possible preceding state to $\mathbf{a}$, we count all ways in which we can reach $\mathbf{a}$ from $\mathbf{a^p}$ with a higher card for player 1, and include the product of that count and $M(\mathbf{a^p})$ in $M(\mathbf{a})$. If we let $P(\mathbf{a})$ name the set of possible preceding states to $\mathbf{a}$, and $W(\mathbf{a^p},\mathbf{a})$ count the number of ways of getting from one to the next state by dealing two cards, player 1’s higher, from among those remaining, then:

Suppose we’re calculating $M(3,3,1,2)$. One possible preceding state is $(4,3,2,2)$. To get to the new state without matching, we can choose any of the $6$ cards in the three-of-the-value group and any of the $6$ in the two-of-the-value group, and assign player 1 the higher card. So the number of ways of arriving perfectly at $(3,3,1,2)$ having previously been at $(4,3,2,2)$ is $36 \cdot M(4,3,3,2)$.

There are, it turns out, $1199$ game states to consider, so we will rely on the computer. The code below implements this, quickly yielding an expectation of $159,620,172$ deals before a perfect one (twice that if we are counting only wins by one player).

Retaining the assumption of four cards per value, the expectation for a perfect game seems to be exponential with the number of card values, as can be seen here (the vertical axis is on a log scale).

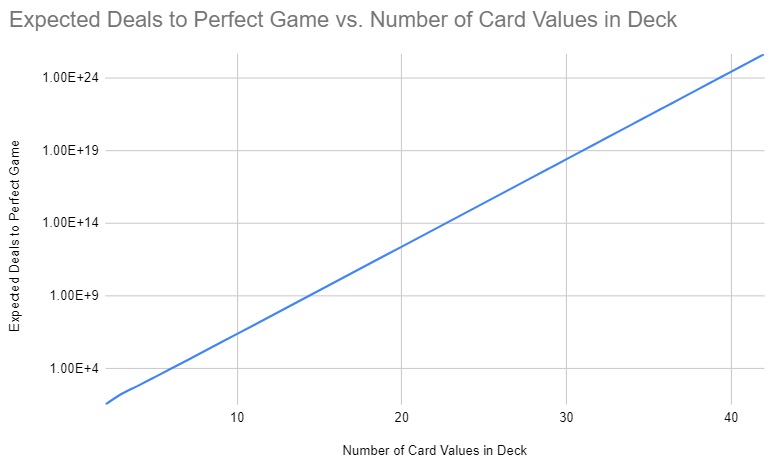
Now, the count of perfect games varies with the count of games in which there is no match in the first deal in a simple way: there are $2$ raised to twice minus one of the number of card values as many of the latter. So that’s a source of exponentiality. And it seems to be the only such source. The expectation of the first game with no matches in the first run-through seems to approach a limit somewhere below 4.56. I have a hunch that Euler would find $e$ in there somewhere.

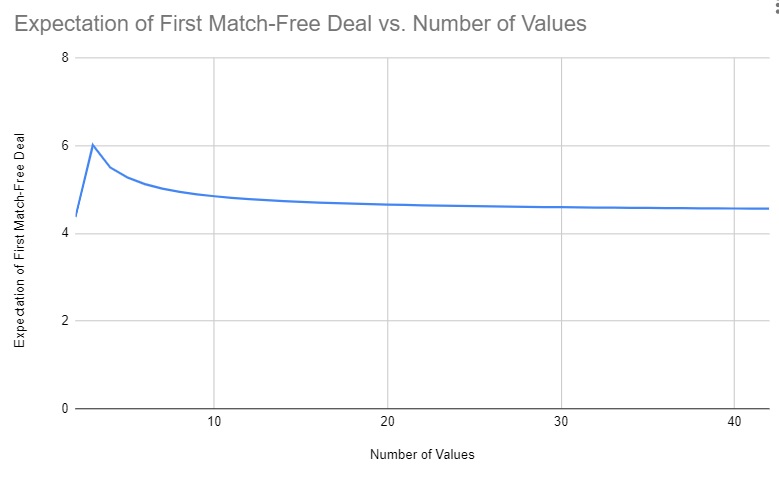
(No, it’s not exactly 6 at $n = 3$.) Thanks to Angela Zhou for the important suggestion to memoize the recursion.

from math import factorial

# Return number of ways to deal perfectly for player 1
# from a state (a,b,c,d) where among remaining cards 
# are a,b,c,d card values with 1,2,3,4 each to
# final state (0,0,0,0)
def perfectDealsFrom (state):
	global alreadyDone
	if state in alreadyDone:
		return alreadyDone[state]
	totalWaysFromHere = 0
	# index of first card
	for i in range(4):
		if state[i] == 0:
			continue
		# choose among i+1 cards each of state[i] values
		choicesOfCard1Card = (i + 1) * state[i]
		stateAfterCard1 = list(state)
		stateAfterCard1[i] -= 1
		if i > 0:
			stateAfterCard1[i-1] += 1
		card1ValueNowAt = i - 1
		# index of second card
		for j in range(4):
			if (stateAfterCard1[j] == 0) or (stateAfterCard1[j] == 1 and card1ValueNowAt == j):
				continue
			if card1ValueNowAt == j:
				choicesOfCard2 = (j + 1) * (stateAfterCard1[j] - 1)
			else:
				choicesOfCard2 = (j + 1) * stateAfterCard1[j]
			stateAfterCard2 = list(stateAfterCard1)
			stateAfterCard2[j] -= 1
			if j > 0:
				stateAfterCard2[j-1] += 1
			# divide by two because half of these choices give player 1 the lower card
			choicesOfBothCards = choicesOfCard1Card * choicesOfCard2 / 2
			totalWaysFromHere += choicesOfBothCards * perfectDealsFrom(tuple(stateAfterCard2))
	alreadyDone[state] = totalWaysFromHere
	return totalWaysFromHere

alreadyDone = { (0,0,0,0) : 1 }
numCardValues = 13

numPerfectDeals = perfectDealsFrom((0,0,0,numCardValues))
print("Number of perfect deals for player 1",numPerfectDeals)
totDeals = factorial(4*numCardValues)
print("Total number of deals:",totDeals)
probPerfect = numPerfectDeals/totDeals
print("Probability of a perfect deal won by player 1:", probPerfect)
print("Expected deals until a perfect deal won by player 1:", 1/probPerfect)
print("Expected deals until a perfect deal:", 1/(2*probPerfect))

Number of perfect deals 2.5265658566028886e+59
Total number of deals: 80658175170943878571660636856403766975289505440883277824000000000000
Probability of a perfect deal won by player 1: 3.132436174322294e-09
Expected deals until a perfect deal won by player 1: 319240343.4098226
Expected deals until a perfect deal: 159620171.7049113
[Finished in 0.3s]