On the table in front of you are two coins. They look and feel identical, but you know one of them has been doctored. The fair coin comes up heads half the time while the doctored coin comes up heads 60 percent of the time. How many flips — you must flip both coins at once, one with each hand — would you need to give yourself a 95 percent chance of correctly identifying the doctored coin?
Extra credit: What if, instead of 60 percent, the doctored coin came up heads some $p$ percent of the time? How does that affect the speed with which you can correctly detect it?
Solution
The extra credit seems no harder than the original, so we’ll work with coins $C_1$ and $C_2$ of weights $p_1$ and $p_2$ such that $p_1 < p_2$, and we count as “detecting” if there are more heads with $C_2$. So our question is, how likely is there to be more heads with $C_2$ in $n$ flips of each?
Where ${i \choose j}$ means the number of ways of choosing $j$ out of $i$ things, the probability that a coin with chance $p$ of heads, in $n$ flips, produces $m$ heads is given by the binomial distribution:
\[B_{p,n,m} = {n \choose m}p^m(1-p)^{n-m}\]This is because for each way of choosing $m$ of the coins to be the heads, the probability that each of those coins would come up heads is $p^m$ and the probability that all of the others would come up tails is $(1-p)^{n-m}$.
So the probability that $C_2$ has more heads than $C_1$ is:
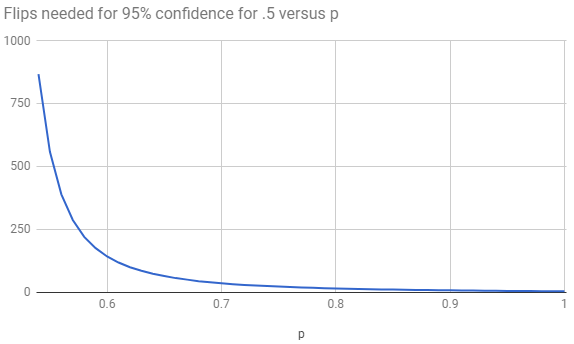
\[\sum_{i=0}^{n-1} \sum_{j=i+1}^{n} B_{p_1,n,i}B_{p_2,n,j}\]Calculating this for the case of $.5$ and $.6$ is feasible in Python, and it yields a probability over .95 first at $n=143$. For a $p_2$ value below $.6$, $n$ gets high enough that the combinatorics are too large for Python, and so we rely on the normal approximation to the binomial distribution:
\[N_{p,n,m} = \frac{1}{\sqrt{2\pi\sigma^2}\exp\left( (m-\mu)^2/2\sigma^2 \right)}\]where $\mu$ is the mean $np$ and $\sigma^2$ is the variance $np(1-p)$.