Bridged Islands

It’s not quite “Waterworld” yet, but the only land humanity has left is a bunch of circular islands where each continent used to be. Fortunately, we have some good engineers. We are planning to connect the islands to each other through a network of straight-line bridges. But, of course, there are rules:

The bridges cannot cross each other or pass over islands, and can only be placed horizontally (east-west) or vertically (north-south). (Diagonal bridges are too difficult for your engineers to build.)

A pair of islands can’t be connected by more than two bridges.

All the islands must be connected together in a single, contiguous group. In other words, the people on any given island need to be able to reach every other island, even if they have to take a circuitous route. Each island (represented by a circle on the diagrams below) has a value equal to the total number of bridges that connect it to its neighbors.

To connect the islands appropriately, you’ll need to follow the diamond-shaped signs sprinkled throughout this dystopia. Each corner of the sign corresponds to one of the four directions (north, south, east, west), and the numbers in those corners show the sum of the values of the islands that lie on a straight line extending in that direction. No value can be repeated within a single sum — for example, if the sum is 10, the values that make it up cannot be 5 and 5.

The bridges cannot pass through the signs. One sign on each continent is no longer displaying numbers, and nobody remembers the whole layout anymore. How are we going to build the bridges?

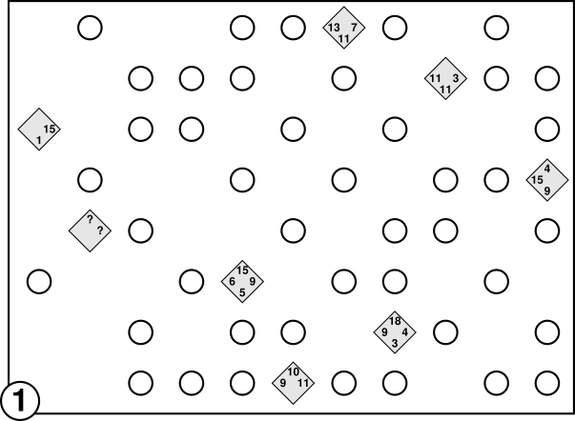
Puzzle map.

(fivethirtyeight)

These puzzles (there are seven similar maps in addition to this one) were part of the 2018 MIT Mystery Hunt.

Solution:

I solved the first map (displayed here) manually, and decided that these puzzles are fun, but not let’s-do-eight-in-a-row fun. So I turned to the computer with a welcome excuse to try out Google’s Constraint Programming package, which can be used from within Python:

from ortools.constraint_solver import pywrapcp

We encode the maps in two parts. The first is a list of the coordinates of every island in the map (which is an 11 by 8 grid), and the second is a dictionary data structure assigning to the coordinates of each sign a list of four numbers, which are the north, south, east and west numbers on the sign (0 means there is no number):

Width = 11
Height = 8

# Map 1 data
Islands = ((0,2),(1,4),(1,7),(2,0),(2,1),(2,3),(2,5),(2,6),(3,0),(3,2),(3,5),(3,6),(4,0),(4,1),(4,4),(4,6),(4,7),(5,1),(5,3),(5,5),(5,7),(6,0),(6,2),(6,4),(6,6),(7,0),(7,2),(7,3),(7,5),(7,7),(8,1),(8,3),(8,4),(9,0),(9,2),(9,4),(9,6),(9,7),(10,0),(10,1),(10,3),(10,5),(10,6))
Signs = {(0,5):(0,1,15,0),(1,3):(0,0,0,0),(4,2):(15,5,9,6),(5,0):(10,0,11,9),(7,1):(18,3,4,9),(8,6):(0,11,3,11),(10,4):(4,9,0,15)}

Before bringing in the CP solver, we take care of a few preliminaries. First, we find every island’s bridgeable neighboring islands:

Neighbors = {}
for Island in Islands:
  Neighbors[Island] = []
  x,y = Island
  for x1,x2,y1,y2,xStep,yStep in ((x+1,Width,y,y+1,1,1),(x-1,-1,y,y+1,-1,1),(x,x+1,y+1,Height,1,1),(x,x+1,y-1,-1,1,-1)):
    Done = False
    for xx in range(x1,x2,xStep):
      for yy in range(y1,y2,yStep):
        if (xx,yy) in Islands:
          if not Done:
            Neighbors[Island].append((xx,yy))
            Done = True
        elif (xx,yy) in Signs:
          Done = True

Next, we locate every case where bridges might cross one another, and we keep a list of these:

CrossThreats = []
for (x1,y1) in Islands:
  for (x2,y2) in Islands:
    for (x3,y3) in Islands:
      for (x4,y4) in Islands:
        if y2>=y1 or not x1==x2 or x3>=x4 or not y3==y4 or x1<=x3 or x1>=x4 or y3>=y1 or y3<=y2:
          continue
        if (x2,y2) in Neighbors[(x1,y1)] and (x4,y4) in Neighbors[(x3,y3)]:
          CrossThreats.append(((x1,y1),(x2,y2),(x3,y3),(x4,y4)))

Now we bring in CP by creating a solver object:

solver = pywrapcp.Solver("")

Next we create the solver variables with which we will formulate the problem for the solver. For instance, the value, or number of bridges on, island (2,1) is represented by the solver variable with the name IslandValue_2_1. That solver variable is the value of our Python variable Value[(2,1)]. Our creation of the variable builds in the constraint that the value be an integer between 1 and 8.

Vars = []

## Island values (number of bridges)
Value = {}
for Island in Islands:
  Value[Island] = solver.IntVar(1,8,"IslandValue_"+str(Island[0])+"_"+str(Island[1]))
  Vars.append(Value[Island])

We also have variables to represent the number of bridges between pairs of neighboring islands (an integer between 0 and 2):

BridgesBetween = {}
for Island in Islands:
  x,y = Island
  for Neighbor in Neighbors[Island]:
    x1,y1 = Neighbor
    if x<x1 or (x==x1 and y<y1):
      BridgesBetween[(Island,Neighbor)] = solver.IntVar(0,2,"BridgesBetween_"+str(x)+"_"+str(y)+"_"+str(x1)+"_"+str(y1))
      Vars.append(BridgesBetween[(Island,Neighbor)])

Now we have to state the rules of the puzzle as constraints on the values of these variables. The first constraint is that the value of an island is the number of bridges from it to its neighbors.

for Island in Islands:
  Bridges = []
  for Neighbor in Neighbors[Island]:
    if (Island,Neighbor) in BridgesBetween:
      Bridges.append(BridgesBetween[(Island,Neighbor)])
    else:
      Bridges.append(BridgesBetween[(Neighbor,Island)])
  solver.Add(Value[Island] == sum(Bridges))

The second and third constraints are that the sums indicated by the signs are correct, and that no addends are repeated.

def FindAddends(x1,x2,y1,y2,xStep,yStep,Tot):
  Addends = []
  xx,yy = x1,y1
  while not (xx==x2 or yy==y2):
    if (xx,yy) in Signs:
      break
    if (xx,yy) in Islands:
      Addends.append(Value[(xx,yy)])
    xx += xStep
    yy += yStep
  solver.Add(sum(Addends) == Tot)
  solver.Add(solver.AllDifferent(Addends))

for Sign in Signs:
  x,y = Sign
  N,S,E,W = Signs[Sign]
  if not N == 0:
    FindAddends(x,x+1,y+1,Height,0,1,N)
  if not S == 0:
    FindAddends(x,x+1,y-1,-1,0,-1,S)
  if not E == 0:
    FindAddends(x+1,Width,y,y+1,1,0,E)
  if not W == 0:
    FindAddends(x-1,-1,y,y+1,-1,0,W)

The bridges must not cross, and so for every two pairs of islands threatening a cross, the number of bridges between the islands in at least one of the pairs must be 0.

for Island1,Island2,Island3,Island4 in CrossThreats:
  solver.Add(BridgesBetween[(Island2,Island1)]*BridgesBetween[(Island3,Island4)] == 0)

We create a “decision builder,” specifying some parameters of the solver’s strategy.

db = solver.Phase(Vars, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)

Finally we call the solver, and hope for the best. There may be multiple solutions consistent with our constraints; we wait for one that yields a connected map: one where you can get from any island to any other.

if solver.Solve(db):
  while solver.NextSolution():
    if Connected(BridgesBetween):
      print("Solution:")
      for Island in Islands:
        print("Island", Island, "=",Value[Island].Value())
      for B in BridgesBetween:
        print(B,BridgesBetween[B].Value(), "bridges")
      break

Here’s how the function Connected is defined (it’s a depth-first search):

# Test whether the map is a connected graph.
def Connected(BridgesBetween):
  global Islands, Neighbors
  
  def Explore(Island):
    Remaining.remove(Island)
    if Remaining == []:
      return
    else:
      for Neighbor in Neighbors[Island]:
        if not Neighbor in Remaining:
          continue
        if (Island,Neighbor) in BridgesBetween:
          Pair = (Island,Neighbor)
        else:
          Pair = (Neighbor,Island)
        if BridgesBetween[Pair].Value() == 0:
          continue
        Explore(Neighbor)

  Remaining = list(Islands)
  Explore(Remaining[0])
  return (not Remaining == [])

I didn’t know whether the complexity of these puzzles would overwhelm CP, but in fact this code solves a map within a couple of seconds.

The whole program is here, and the output as run on map 1 is here.