You know the following things about the delicate ecology of scorpions and meerkats:
- If there were no meerkats, the population of the scorpions would double every month. 2.If there were no scorpions, the population of the meerkats would halve every month. 3.If you had exactly 20 scorpions and five meerkats, both populations would not change at all.
What is the number of meerkats when the desert has as many scorpions as possible?
What is the number of meerkats and the number of scorpions when the meerkat population is increasing by four meerkats per month and the scorpion population is decreasing by two scorpions per month?
These questions rely on the Lotka-Volterra model of predators and prey. That model makes certain assumptions, including that the prey (the scorpions here) always find ample food, the predators (the meerkats) have limitless appetite, and the rate of change of a population is proportional to its size.
Extra credit: If you start with 100 scorpions and 10 meerkats, what is the maximum number of meerkats you can have and how long would it take for both populations to return to their starting states?
Solution
Let the numbers of meerkats and scorpions at time $t$ be $m_t$ and $s_t$. The Lotka–Volterra equations give us:
\[\frac{dm_t}{dt} = \delta m_t s_t - \gamma m_t\] \[\frac{ds_t}{dt} = \alpha s_t - \beta m_t s_t\]When $s = 0$, the meerkats halve every month:
\[m_t = m_0 2^{-t}\] \[\frac{dm_t}{dt} = -\gamma m_t = m_0 \times -\ln(2)2^{-t} = -\ln(2)m_t\]And so $\gamma = \ln(2)$.
Similarly, when $m = 0$:
\[s_t = s_0 2^t\] \[\frac{ds_t}{dt} = \alpha s_t = s_0 \ln(2)2^t = \ln(2)s_t\]And so $\alpha = \ln(2)$.
When $m = 5$ and $s = 20$, we are told that the populations will not change. It follows that the derivatives of $m_t$ and $s_t$ are zero for those values. Therefore:
\[100 \delta - 5\ln(2) = 0 \Rightarrow \delta = \frac{\ln(2)}{20}\] \[20\ln(2) - 100\beta = 0 \Rightarrow \beta = \frac{\ln(2)}{5}\]Thus, the differential equations become:
\[\frac{dm_t}{dt} = \frac{\ln(2)}{20} m_t s_t - \ln(2) m_t\] \[\frac{ds_t}{dt} = \ln(2) s_t - \frac{\ln(2)}{5} m_t s_t\]The first question asks, “What is the number of meerkats when the desert has as many scorpions as possible?”
The puzzle here is to figure out what that question means. Maybe its a trick question: there are zero meerkats when the scorpion populations explodes without bounds. Otherwise, the answer seems to be that there is no limit to the number of scorpions, nor to the number of meerkats.
The second question asks, “What is the number of meerkats and the number of scorpions when the meerkat population is increasing by four meerkats per month and the scorpion population is decreasing by two scorpions per month?” Here we simply solve two simultaneous equations in the two variables $m_t$ and $s_t$, which yields a quadratic equation whose positive solution contains about $5$ meerkats and $42$ scorpions.
Finally, “Extra credit: If you start with 100 scorpions and 10 meerkats, what is the maximum number of meerkats you can have and how long would it take for both populations to return to their starting states?”
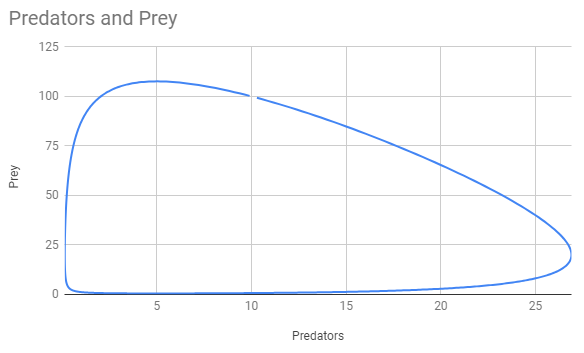
The Wikipedia page on Lotka-Volterra Systems tells us that from starting points in the northeast quadrant of the plane whose axes are the numbers of predators and prey, the populations will trace a closed circuit around the non-zero equilibrium point (which in our case is $(5,20)$).
Integrating numerically (code below), we find that starting with $(10,100)$, we trace a full circuit every $13.45$ months, reaching a maximum of $26.90$ predators. However, the numbers of predators and of prey dip below $1$ each cycle before recovering, so if we don’t want to allow regenerating, proper critter parts into our model’s ontology, it may be best to think of this as counting population by thousands, millions, or the like.
Code (Python):
from math import log
STEPSPERMONTH = 100000000
START = (100,10)
A = C = log(2)
B = log(2)/5
D = log(2)/20
prey,predators = START
time = 0
farFromHome = False
maxPredators = 0
while True:
step = 1.0/STEPSPERMONTH
oldPredators = predators
predators += step*(D*predators*prey - C*predators)
if predators > maxPredators:
maxPredators = predators
prey += step*(A*prey - B*predators*prey)
time += 1
if (not farFromHome) and abs(prey-START[0]) > .1:
farFromHome = True
if farFromHome:
if abs(prey-START[0]) < .0001 and abs(predators-START[1]) < .0001:
break
print "Max predators is",maxPredators,"and period is",1.0*time/STEPSPERMONTH,"months"