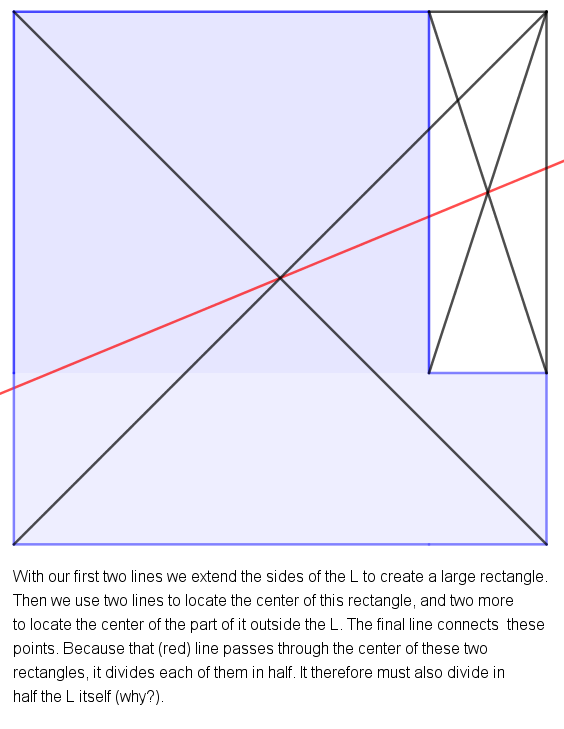
Say you have an “L” shape formed by two rectangles touching each other. These two rectangles could have any dimensions and they don’t have to be equal to each other in any way.
Using only a straightedge and a pencil (no rulers, protractors or compasses), how can you draw a single straight line that cuts the L into exactly two pieces of exactly equal area, no matter what the dimensions of the L are? You can draw as many lines as you want to get to the solution, but the bisector itself can only be one single straight line.