Perfect War

Assuming a deck is randomly shuffled before every game, how many games of War would you expect to play until you had a game that lasted just 26 turns?

fivethirtyeight.

Solutionish Musings

There are $52!$ different, equally likely deals. If we can find the number of match-free deals, which result in a $26$-turn game, we can divide the former by the latter number to get our answer (which is the inverse of the probability of getting a $26$-turn game).

We will use a recurrence to calculate the number of match-free, perhaps partial deals that lead to a given game state, where a state lists the number of card values of which just one remains, two remain, and so on. So we’ll use $M(a_1,a_2,a_3,a_4)$, or $M(\mathbf{a})$, to mean the number of match-free deals that get you to $\mathbf{a}$, starting from $(0,0,0,13)$. Our goal is to find $M(0,0,0,0)$, the number of match-free deals of the whole deck. Of course $M(0,0,0,13)$ is $1$.

We can calculate values of $M(\mathbf{a})$ from those of $M$ at preceding states. $M(\mathbf{a})$ is a sum: for each $\mathbf{a^p}$ that describes a possible preceding state to $\mathbf{a}$, we count all ways in which we can match-freely reach $\mathbf{a}$ from $\mathbf{a^p}$, and include the product of that count and $M(\mathbf{a^p})$ in $M(\mathbf{a})$. If we let $P(\mathbf{a})$ name the set of possible predecessor states to $\mathbf{a}$, and $W(\mathbf{a^p},\mathbf{a})$ count the number of ways of getting from one to the next state by dealing two among the remaining cards, then:

Suppose we’re calculating $M(3,3,1,2)$. One possible preceding state is $(4,3,2,2)$. To get to the new state without matching, we can choose any of the $6$ cards in the three-of-the-value group and any of the $6$ in the two-of-the-value group, and distribute these two cards in either of the two possible ways. So the number of ways of arriving match-freely at $(3,3,1,2)$ having previously been at $(4,3,2,2)$ is $72 \cdot M(4,3,3,2)$.

The code below (if correct!) does this for every possible match-free deal, and yields an expectation of 6.446976545663825e+16 deals before a match-free one. (Thanks to Angela Zhou for prompting me to memoize (the “alreadyDone” part).)

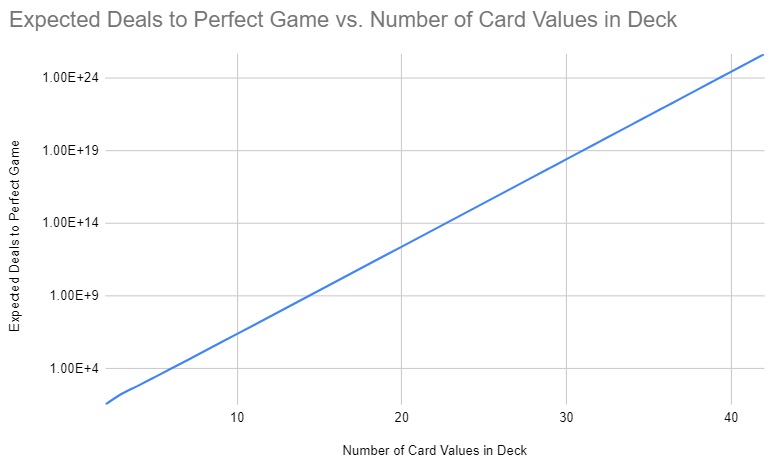
The expectation seems to be roughly proportional to the log of the number of card values in the deck. Maybe that’s a worthy echo of Euler’s amazing result about the somewhat similar, but evidently importantly different, Game of Coincidence.

from math import factorial

# Return number of ways to deal matchlessly from a state [a,b,c,d] where
# among remaining cards are a,b,c,d card values with 1,2,3,4 cards to
# final state [0,0,0,0]
def matchlessDealsFrom (state):
	global alreadyDone
	if state in alreadyDone:
		return alreadyDone[state]
	totalWaysFromHere = 0
	for i in range(4):
		# index of player 1's next card
		if state[i] == 0:
			continue
		# choose among i+1 cards each of state[i] values
		waysFromHere = (i + 1) * state[i]
		newState = list(state)
		newState[i] -= 1
		if i > 0:
			newState[i-1] += 1
		firstValueAt = i - 1
		for j in range(4):
			# index of player 2's card
			if newState[j] == 0 or (newState[j] == 1 and firstValueAt == j):
				continue
			if j == firstValueAt:
				waysFromHere *= (j + 1) * (newState[j] - 1)
			else:
				waysFromHere *= (j + 1) * newState[j]
			newState[j] -= 1
			if j > 0:
				newState[j-1] += 1
			totalWaysFromHere += waysFromHere * matchlessDealsFrom(tuple(newState))
	alreadyDone[state] = totalWaysFromHere
	return totalWaysFromHere

alreadyDone = { (0,0,0,0) : 1 }
numCardValues = 13
numMFDeals = matchlessDealsFrom((0,0,0,numCardValues))
print("Number of match-free deals:", numMFDeals)
print("Probability of a match-free deal:", numMFDeals/factorial(4*numCardValues))
print("Expected deals until a match-free one:", factorial(4*numCardValues)/numMFDeals)
print(factorial(52)/matchlessDealsFrom((0,0,0,13)))

Number of match-free deals: 1251100800501497113857212829658012657875058006425600
Probability of a match-free deal: 1.5511146859570794e-17
Expected deals until a match-free one: 6.446976545663825e+16
[Finished in 0.6s]