What’s the smallest tetrahedron into which we can pack four spheres?
Solution
I’ll assume without proof what seems obvious, namely, that the optimal configuration of the spheres is all-touching, so that their centers form a smaller regular tetrahedron, and that three spheres are tangent to each face (as drawn on the fiverthirtyeight post). Here’s a view of one of the spheres inside the tetrahedron so-constructed.
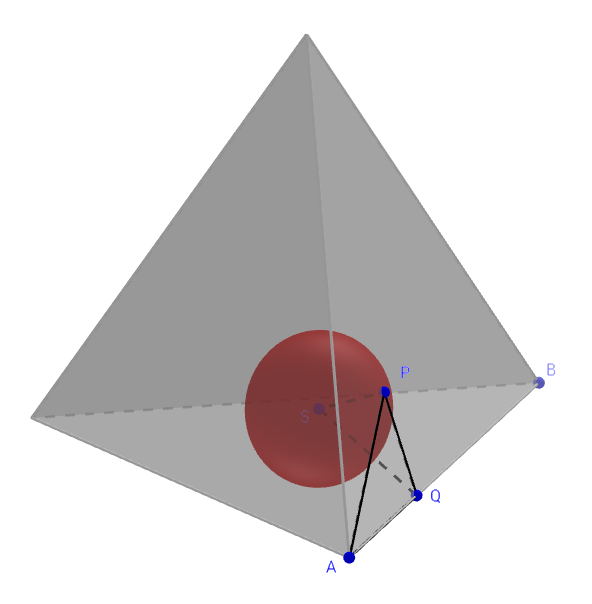
Pick an edge AB of the tetrahedron; we will find a formula for its length. Draw a line from A to the point P on an adjacent face where the nearest sphere (with center S) touches that face, and draw the line from P to a point Q on AB so that PQ is perpendicular to AB. The length of AB is $2r$ (two radii of the spheres) plus twice the length of AQ.
Since APQ is a 30-60-90 right triangle, AQ is $\sqrt{3}$ times as long as PQ, so let’s find that length. Angle PQS is half the dihedral angle of the tetrahedron and hence (as we saw a couple of weeks ago) has sine $1/\sqrt{3}$ and hence tangent $1/\sqrt{2}$. Thus PQ is $r\sqrt{2}$ long, and $AQ$ is $r\sqrt{6}$ long, giving the tetrahedron a side of $(2+2\sqrt{6})r$, or about $6.90r$.