The famous four-color theorem states, essentially, that you can color in the regions of any map using at most four colors in such a way that no neighboring regions share a color. A computer-based proof of the theorem was offered in 1976.
Some 2,200 years earlier, the legendary Greek mathematician Archimedes described something called an Ostomachion. It’s a group of pieces, similar to tangrams, that divides a 12-by-12 square into 14 regions. The object is to rearrange the pieces into interesting shapes, such as a Tyrannosaurus rex. It’s often called the oldest known mathematical puzzle.
Your challenge today: Color in the regions of the Ostomachion square with four colors such that each color shades an equal area. (That is, each color needs to shade 36 square units.)
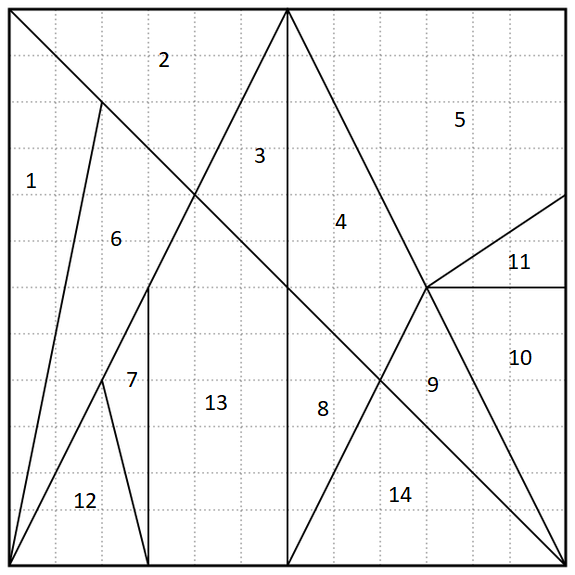
Solution
See the previous post to learn more about the operation of Google’s Constraint Solver that is used here as well. In a flash we learn that there are 9 solutions with all four colors used and two with only three of the four used. That’s counting solutions as equivalent if colors are merely swapped.
# We use Google's Constraint Programming solver to solve the puzzle in a flash.
# Find it at https://developers.google.com/optimization/cp/
from ortools.constraint_solver import pywrapcp
from itertools import permutations
Cells = tuple(range(1,15))
Areas = (0,12,12,6,12,24,12,3,6,6,9,3,6,21,12)
Walls = ((1,2),(1,6),(2,3),(2,6),(3,4),(3,13),(4,5),(4,8),(4,9),(5,11),(6,7),(6,12),(6,13),(7,12),(7,13),(8,13),(8,14),(9,10),(9,14),(10,11))
NColors = 4
Colors = tuple(range(NColors))
# Create the solver.
solver = pywrapcp.Solver("")
# Create the variables.
Vars = []
Color = {}
for Cell in Cells:
Color[Cell] = solver.IntVar(0,len(Colors)-1,"Color_"+str(Cell))
Vars.append(Color[Cell])
# Constraints
for Col in Colors:
c = (sum([Areas[Cell]*(Color[Cell]==Col) for Cell in Cells]) == 36)
solver.Add(c)
for Wall in Walls:
solver.Add(solver.AllDifferent((Color[Wall[0]],Color[Wall[1]])))
# Create the "decision builder"
db = solver.Phase(Vars, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)
# Call the solver and display the unique solutions.
Solutions = []
def NewSolution():
for Solution in Solutions:
for Permute in permutations(Colors):
Same = True
for Cell in Cells:
if not Color[Cell].Value() == Permute[Solution[Cell-1]]:
Same = False
if Same:
return False
return True
if solver.Solve(db):
Count = 0
while solver.NextSolution():
if NewSolution():
Count += 1
Solution = [Color[Cell].Value() for Cell in Cells]
Solutions.append(Solution)
print("Solution",Count,Solution)
else:
print("No solution found.")
The output:
Solution 1 [0, 1, 0, 1, 2, 2, 0, 0, 0, 3, 0, 3, 3, 1]
Solution 2 [0, 1, 0, 1, 2, 2, 0, 0, 3, 0, 3, 3, 3, 1]
Solution 3 [0, 1, 0, 1, 2, 2, 1, 0, 0, 1, 3, 0, 3, 3]
Solution 4 [0, 1, 0, 2, 1, 2, 0, 0, 0, 3, 0, 3, 3, 2]
Solution 5 [0, 1, 0, 2, 1, 2, 0, 0, 3, 0, 3, 3, 3, 2]
Solution 6 [0, 1, 0, 2, 3, 2, 0, 0, 3, 0, 1, 3, 1, 2]
Solution 7 [0, 1, 0, 2, 3, 2, 3, 0, 0, 3, 1, 0, 1, 2]
Solution 8 [0, 1, 0, 2, 3, 3, 1, 0, 0, 1, 2, 0, 2, 1]
Solution 9 [0, 1, 0, 2, 3, 3, 2, 0, 0, 2, 1, 0, 1, 2]
[Finished in 0.3s]