You’ll have to click through to see this one . . .
Solution
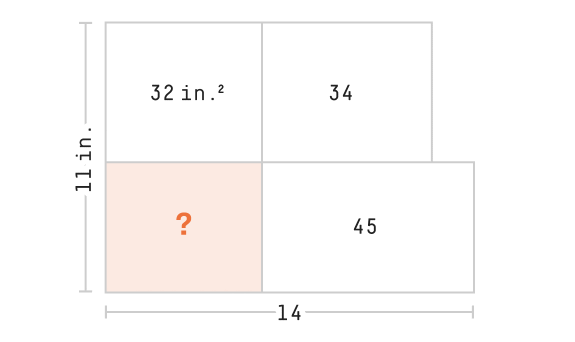
There are numerous ways to show that the answer is $32$. Here are two simple ones:
1.
Call the ``?” area $a$. Then:
\[\frac{32}{a} = \frac{154-32-45-a}{45}\] \[a^2 - 77a + 45\cdot32 = 0\] \[(a-45)(a-32) = 0\] \[a = 45 \mbox{ or } a = 32\]Only $32$ is possible, because $a$ plus $34$ can be at most $154-32-45$, or $77$.
2.
Notice that the boxes of area $32$ and $45$ together take up half of the area of the $11$ by $14$ rectangle containing them. It’s easy to see that boxes formed in this way, sharing a corner point, occupy half the total area iff the corner point is on at least one of the horizontal and vertical bisectors. If the corner point is in the upper left or lower right quadrants, the boxes will take up more than half the area, and if in the other two quadrants, less than half.
If our corner point is on the vertical bisector, then the lower left box has the same area as the lower-right, that is, $45$, which we have seen is impossible. So the corner point is on the horizontal bisector and the area of the lower left box is the same as that of the upper-left, namely, $32$.