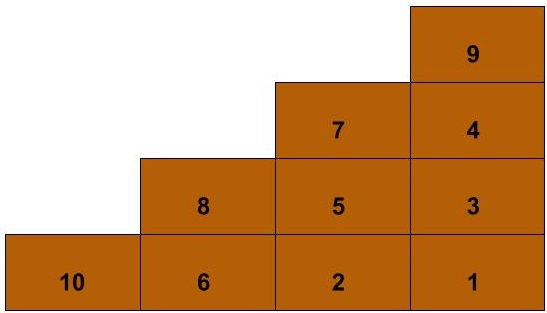
Suppose you have precisely enough blocks to build a staircase with $n$ steps, each $1$ block deep and tall. Given that you must build rows and columns of the blocks up from the floor and out from the wall, how many distinct ways are there to build this staircase?
Solution
For $n$ steps we will need $N = n(n+1)/2$ blocks, which we will number from $1$ to $N$. For any block in the staircase, its hook is the L-shaped set of blocks that includes itself as well as all those later in the same row or the same column. The number of blocks in a block’s hook is its hook length. The hook length of the block in row $i$ and column $j$ (where the first-placed block is $(1,1)$) is:
\[h_{i,j} = 2n + 3 - 2(i+j)\]For the numbering on a completed staircase to be a possible outcome of placing the blocks in numerical order, it is necessary and sufficient that the number on each block is the lowest in its hook. Such staircases fit the definition of standard Young tableaux, and so the number of ways to build an $n$-step staircase is given by the beautifully simple hook length formula:
\[\frac{N!}{\prod_{i,j}h_{i,j}}\]That’s just the total number ways of numbering the blocks in the staircase divided by the product of the blocks’ hook lengths.
Simple as this may be, the proofs of the fact that I have so far seen, including this elegant one, are a little too complex for rehearsing here. But maybe this is a rare case in which a fallacious “proof” (due to Don Knuth) will be enough to convince you of its plausibility. Among all ways of numbering the blocks in the staircase, the odds that a given block will have the lowest number in its hook are $1$ over its hook length, and so (?) the number of ways of numbering staircases wherein all blocks are numbered the lowest in their hooks is the total number of numbered staircases divided by the product of hook lengths. This reasoning is mistaken (as I’m sure Knuth knew) in that whether distinct blocks are numbered lowest in their hooks is not in general probabilistically independent, so multiplying the probabilities is not justified. For example, in a $100$-step staircase, if block $(2,1)$ is the lowest in its hook, its number is likely very low, and so block $(1,1)$ is unlikely to be numbered lower, which it would have to be to be the lowest in its hook.
Since hook length (for a given $n$) depends only on the value $i+j$ (which is shared among blocks on a diagonal) we can simplify a bit. There is always just one block where that value is $2$ (the first block), two where it is $3$, and so on up to $n$ blocks where it is $n+1$. So the product of hook lengths is:
\[(2n + 3 - 2 \times 2)^1 \times (2n + 3 - 2 \times 3)^2 \times \cdots \times (2n + 3 - 2 \times (n+1))^n\] \[= \prod_{k=1}^{n} (2n - 2k + 1)^k\]So our final expression for the number of ways to build an $n$-step staircase is:
\[\frac{N!}{\prod_{k=1}^{n} (2n - 2k + 1)^k}\]This value increases rapidly with the number of steps.
| Steps | Ways |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 16 |
| 4 | 768 |
| 5 | 292864 |
| 6 | 1100742656 |
| 7 | 48608795688960 |
| 8 | 29258366996258488320 |
(I didn’t know about the hook formula for Young tableaux prior to this. I generated the first few values computationally, and then went to OEIS.org, where the formula is mentioned.)
limitN = 10
def findExtensions(seq,N,counts):
if len(seq) == N * (N+1) / 2:
results[N]+= 1
return
for i in range(1,N+1):
if counts[i] + 1 <= counts[i+1] and counts [i] + 1 <= i:
newCounts = list(counts)
newCounts[i] += 1
newSeq = list(seq)
newSeq.append(i)
findExtensions(newSeq,N,newCounts)
results = [0]*(limitN + 1)
for N in range(1,limitN + 1):
seq = [N]
counts = [0]*(N) + [1,N]
findExtensions(seq,N,counts)
print(N,results[N])